The Miracle of Compound Returns
Course Outline
The Miracle of Compound Returns
In this video, we use the miracle of compounding to explain why it’s so important to save early and often.
Consider these two scenarios:
First, meet Myopic Mary. She starts saving in her 30s, and by 45 years old she has $20K. Her intended retirement age is 65. Mary invests her money in a retirement fund with a 7% annual rate of return. She doesn’t touch the money until retirement. How much will she have by then? To get our answer, we’ll use the Rule of 70.
The Rule of 70 lets you approximate the time it’ll take for an investment to double, given a specified rate of return. To apply this rule, you divide 70 by the rate of return, and it’ll tell you the years needed for the doubling. In Myopic Mary’s case, her investment will double every decade.
With 20 years to save, she’ll have roughly $80K by retirement.
Imagine though, that Myopic Mary goes back in time, becoming Meticulous Mary.
Meticulous Mary starts saving in her twenties. By 35, she has the same $20K to invest for retirement. Based on the Rule of 70, it’ll still take 10 years for her money to double. But Meticulous Mary has a longer time horizon, from 35 to 65 years old. Thus, her money will double three times. Her final investment value will be $160K, compared to Myopic Mary’s $80K.
That improved result comes through the miracle of compounding. Compounding gives you defined points where your money grows exponentially. The longer the time horizon, the more growth that occurs.
Now—where does opportunity cost fit into this? Well, for every dollar Myopic Mary invested at 45, that turned into four dollars by the time she was 65. For Meticulous Mary, every dollar invested at 35, turned into eight dollars by retirement. That’s called winning the opportunity cost battle, through compounding.
Like we said, the right course is to save early and save often.
Want to learn more about savings? In future videos we’ll tackle some savings tips and common retirement plans.
Teacher Resources
Related to this course
See all Teacher Resources related to this course
Transcript
Previously, we learned about opportunity cost. But how can this concept help us save smartly? We'll dive into an example illustrating the miracle of compounding, and use opportunity cost to understand the importance of saving and investing early and often. Let's take these two investment scenarios.
In the first scenario, meet Myopic Mary. She starts saving in her 30s, and by age 45 has $20,000. She then invests this money in a retirement fund that earns a 7% annual rate of return and doesn't touch her investment until retirement. How large will Myopic Mary's $20,000 grow to be if it's growing at 7% for 20 years, until she turns 65? For simplicity, we'll use the Rule of 70, which allows you to quickly approximate how long it will take for an investment to double in value given a specified rate of return.
To see how many times Myopic Mary's $20,000 will double, simply divide 70 by the rate of return or growth. So 70 divided by a rate of return of 7 equals 10, which means her money doubles approximately once every 10 years. Since she's investing for 20 years, her money doubles twice. Myopic Mary's $20,000 doubles to roughly $40,000 by the time she's 55, and doubles yet again to $80,000 by the time she's 65 and ready to retire. So she started with $20,000, did not save a single cent more, reinvested her returns, and, after 20 years, ended up with about $80,000. Not too bad!
Now, onward to scenario two. Imagine Myopic Mary goes back in time 10 years, and becomes Meticulous Mary. Meticulous Mary starts saving in her 20s so that by age 35 she has $20,000. At this point, she invests her money in a retirement fund that earns a 7% annual rate of return and doesn't touch her investment until retirement. Our Rule of 70 calculations are exactly the same as scenario one. Given a 7% annual rate of return, Meticulous Mary's money will double every 10 years. The only difference from scenario one is that Meticulous Mary's money will double three times instead of two times. She now has 30 years until retirement, instead of 20. Meticulous Mary's $20,000 will double to $40,000 by the time she's 45, will double again to $80,000 by the time she's 55, and will double yet again, to $160,000, by the time she's 65.
So, let's recap. Both Marys, Meticulous and Myopic, invested the exact same amount, $20,000, at the exact same rate of return, 7%. The only difference between these two scenarios is time. Meticulous Mary started investing just 10 years earlier, and that led to $80,000 more dollars. How can that be? It's the miracle of compounding! Meticulous Mary started saving earlier, and that means that when her investment reached $80,000, she had one more 10-year period, one more doubling period still to go. And it's that last doubling that is the biggest doubling.
When people start to save, it often seems slow and pointless, because things don't change all that much. The rate of absolute change gets faster and faster. This is what people mean by exponential growth. And keep in mind, Meticulous Mary stopped saving at 35. Imagine if she had continued contributing to her retirement fund until she retired. That would be an extra 30 years of additional savings, and additional compound returns.
Now let's think about this through the lens of opportunity costs. Every dollar Meticulous Mary had and invested at 35 turned into $8 by the time she was 65. Contrast this with poor Myopic Mary. Every dollar she had and invested at 45 only turned into $4 at 65. Quite the difference! But the real takeaway from these two scenarios is not about Meticulous or Myopic Mary. The real takeaway is that you should be saving and investing early and often. And yes, I understand -- saving is hard to do. And where should you even save and invest?
Fear not. We'll cover some helpful saving tips and details about common retirement plans in future videos.
Subtitles
- English
- Spanish
- Chinese
- Hindi
Thanks to our awesome community of subtitle contributors, individual videos in this course might have additional languages. More info below on how to see which languages are available (and how to contribute more!).
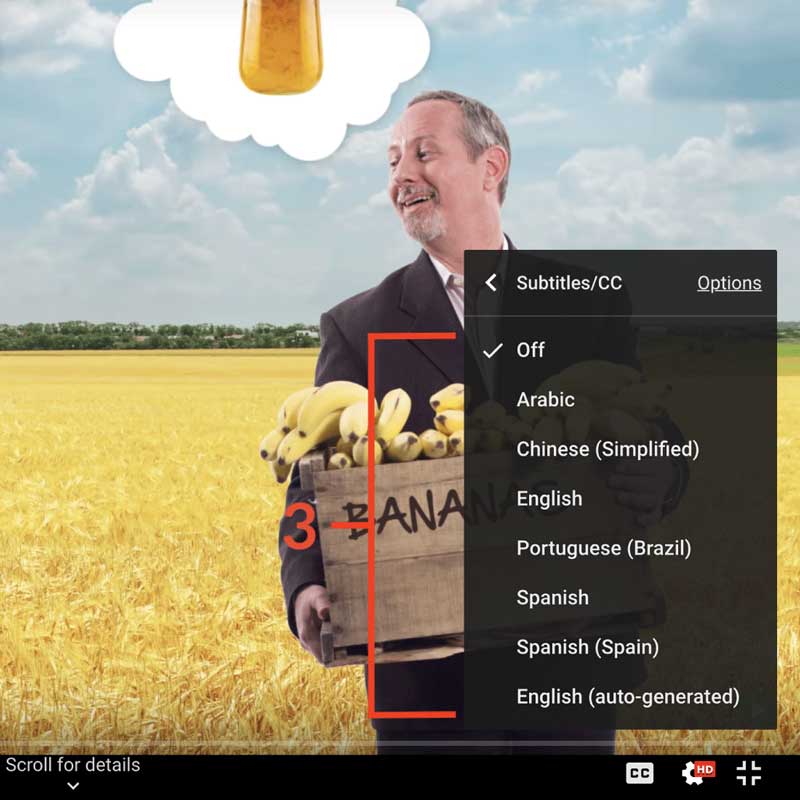
How to turn on captions and select a language:
- Click the settings icon (⚙) at the bottom of the video screen.
- Click Subtitles/CC.
- Select a language.

Contribute Translations!
Join the team and help us provide world-class economics education to everyone, everywhere for free! You can also reach out to us at [email protected] for more info.
Submit subtitles
Accessibility
We aim to make our content accessible to users around the world with varying needs and circumstances.
Currently we provide:
- A website built to the W3C Web Accessibility standards
- Subtitles and transcripts for our most popular content
- Video files for download
Are we missing something? Please let us know at [email protected]
Creative Commons

This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
The third party material as seen in this video is subject to third party copyright and is used here pursuant
to the fair use doctrine as stipulated in Section 107 of the Copyright Act. We grant no rights and make no
warranties with regard to the third party material depicted in the video and your use of this video may
require additional clearances and licenses. We advise consulting with clearance counsel before relying
on the fair use doctrine.
