Calculating the Elasticity of Demand
Course Outline
Calculating the Elasticity of Demand
Elasticity of demand is equal to the percentage change of quantity demanded divided by percentage change in price. In this video, we go over specific terminology and notation, including how to use the midpoint formula. We apply elasticity of demand to the war on drugs, and more broadly to the prohibition of a good when it has an elastic demand.
Teacher Resources
Related to this course
See all Teacher Resources related to this course
Transcript
In our first lecture on the elasticity of demand, we explain the intuitive meaning of elasticity. It measures the responsiveness of the quantity demanded to a change in price. More responsive means more elastic. In this lecture, we're going to show how to create a numeric measure of elasticity. How to calculate with some data on prices and quantities, what the elasticity is over a range of the demand curve.
So here's a more precise definition of elasticity. The elasticity of demand is the percentage change in quantity demanded divided by the percentage change in price. So let's write it like this. We have some notation here. The elasticity of demand is equal to the percentage "change in". Delta is the symbol for change in, so this is the percentage change in the quantity demanded divided by the percentage change in the price. That's the elasticity of demand. Let's give an example or two.
So, if the price of oil increases by 10% and over a period of several years the quantity demanded falls by 5%, then the long run elasticity of demand for oil is what? Well, elasticity is the percentage change and the quantity demanded. That's -5% divided by the percentage change in the price. That's 10%. So the elasticity of demand is -5% divided by 10%, or -0.5. Elasticities of demand are always negative because when price goes up, the quantity demanded goes down. When price goes down, the quantity demanded goes up. So we often drop the negative sign and write that the elasticity of demand is 0.5.
Here's some more important notation. If the absolute value of the elasticity of demand is less than one, just like the example we just gave for oil, we say that the demand curve is inelastic. Elasticity of demand less than one, the demand curve is inelastic. If the elasticity of demand is greater than one, we say the demand curve is elastic. And if elasticity of demand is equal to one, that is the knife point case, then the demand curve is unit elastic. These terms are going to come back, so just keep them in mind. Inelastic: less than one. Elastic: greater than one.
So we know that elasticity is the percentage change in quantity divided by the percentage change in price, how do we calculate the percentage change in something? This is not so hard, but it could be a little bit tricky for the following reason. Let's suppose you're driving down the highway at 100 miles per hour. I don't recommend this, but let's just imagine that you are. You're going 100 miles per hour, and now you increase speed by 50%. How fast are you going? 150 miles per hour, right? Okay, so now you're going 150 miles per hour. Suppose you decrease speed by 50%. Now, how fast are you going? 75 miles per hour, right?
So how is it that you can increase speed by 50% and then decrease by 50% and not be back to where you started? Well the answer is, is that intuitively, we have changed the base by which we are calculating the percentage change. And we don't want to have this inconsistency when we calculate elasticity. We want people to get the same elasticity whether they're calculating from the lower base or from the higher base. So, because of that, we're going to use the Midpoint Formula. So, the elasticity of demand, percentage change in quantity divided by the percentage change in price, that's the change in quantity divided by the average quantity times 100. That will give us the percentage change divided by the change in price divided by the average price. Again, that times 100. Notice, since we've actually got 100 on top and 100 on the bottom, those 100s we can actually cancel out.
Let's expand this just a little bit more. The change in quantity. What is the change in quantity? Well, let's suppose we have two quantities. Let's call them after and before. It doesn't matter which one we call after or which one before. So, we're going to then expand this to the change in quantity. That's Q after minus Q before divided by the average, Q after plus Q before, divided by two, divided by the change in price, P after minus P before, divided by the average price, b after plus b before, divide by two. So that's a little bit of a mouthful, but everything, I think, is fairly simple. Just remember change in quantity divided by the average quantity and you should always be able to calculate this. Let's give an example.
Okay, here's an example of a type of problem you might see on a quiz or a mid term. At the initial price of $10, the quantity demanded is 100. When the price rises to $20, the quantity demanded falls to 90. What is the elasticity is, what is the elasticity over this range of the demand curve? Well, we always want to begin by writing down what we know -- our formula. The elasticity of demand is the percentage change in quantity divided by the percentage change in price. Now, let's remember to just expand that. That's Delta Q over the average Q all divided by Delta P over the average P.
Now, we just start to fill things in.
So our quantity after, okay, after the change is 90. Our quantity before that was 100. So on the top, the percentage change in quantity is 90 minus 100 divided by 90 plus 100, over two. That is the average quantity. And then on the bottom, and the only trick here is always write it in the same order, so if you put the 90 here, then make sure you put the 20, the number the price which is associated with that quantity started off the same way. So, always just keep it in the same order. So on the bottom, then, we have the quantity -- the price after -- which is 20 minus the price before, which is 10, divided by the average price.
And now, just, it's numerics. You plug in the numbers and what you get is the elasticity of demand is equal to -0.158, approximately. We can always drop the negative sign because these things, elasticity of demands, are always negative. So it's equal to 0.158. So does this make the elasticity of demand over this range elastic or inelastic? Inelastic, right? The elasticity of demand we've just calculated is less than one, so that makes this one inelastic. There you go.
We need to cover one more important point about the elasticity of demand, and that is its relationship to total revenue. So a firm's revenues are very simply equal to price times quantity sold. Revenue is equal to price times quantity. Now, elasticity, it's all about the relationship between price and quantity, and so it's also going to have implications for revenue. Let's give some intuition for the relationship between the elasticity and total revenue. So revenue is price times quantity. Now suppose the price goes up by a lot and then quantity demanded goes down, just by a little bit. What then is going to be the response of revenue? Well, if price is going up by a lot and quantity is going down just by a little bit, then revenue is also going to be going up. Now, what kind of demand curve do we call that, when price goes up by a lot and quantity falls by just a little bit? We call that an inelastic demand curve. So, what this little thought experiment tells us is that when you have an inelastic demand curve, when price goes up revenue is also going to go up, and of course, vice versa.
Let's take a look at this with a graph. So here's our initial demand curve, a very inelastic demand curve, at a price of $10, the quantity demanded is 100 units, so revenue is 1,000. Notice that we can show revenue in the graph by price times quantity. Now, just looking at the graph, look at what happens when the price goes up to 20. Well, the quantity demanded goes down by just a little bit, in this case to 90, but revenues go up to 1,800. So you can just see, by sketching the little graph, what happens to revenues when price goes up when you have an inelastic demand curve. And again, vice versa. Let's take a look about what happens when you have an elastic demand curve.
So let's do the same kind of little thought experiment, revenue is price times quantity. Suppose price goes up by a modest amount and quantity goes down by a lot. Well, if price is going up by a little bit and quantity is going down by a lot, then revenue must also be falling. And what type of demand curve is it when price goes up by a little bit, quantity falls by a lot? What type of demand curve is that? That's an elastic demand curve. So, revenues fall as price rises with an elastic demand curve. And again, let's show that. If you're ever confused and you can't quite remember, just draw the graph. I can never remember, myself, but I always draw these little graphs. So, draw a really flatter, elastic demand curve. In this case, at a price of $10, the quantity demanded is 250 units. So revenues is 2,500. And see what happens, when price goes up, price goes up to $20, quantity demanded falls to 50, so revenue falls to 1,000. And again, you can just compare the sizes of these revenue rectangles to see which way the relationship goes. And of course, this also implies, going from $20, the price of $20 to a price of $10, revenues increase. So with an elastic demand curve, when price goes down, revenues go up.
So here's a summary of these relationships. When the elasticity of demand is less than one, that's an inelastic demand curve and price and revenue move together. When one goes up, the other goes up. When one goes down, the other goes down. If the elasticity of demand is greater than one, that's an elastic demand curve and price and revenue move in opposite directions. And could you guess what happens if the elasticity of demand is equal to one -- if you have a unit elastic curve? Well then, when the price changes, revenue stays the same. Now, if you have to, again, memorize these, but it's really much better to just sketch some graphs. I never remember them, as I've said myself, I never remember these relationships, but I can always sketch an inelastic graph and then with a few changes in price, I can see whether the revenue rectangles are getting bigger or smaller and so I'll be able to recompute all of these relationships pretty easily.
Here's a quick practice question. The elasticity of demand for eggs has been estimated to be 0.1. If egg producers raise their prices by 10%, what will happen to their total revenues? Increase? Decrease? Or it won't change? Okay, how should we approach this problem? If the elasticity of demand is 0.1, what type of demand curve? Inelastic demand. Now, what's the relationship between an inelastic demand curve? When price goes up, what happens to revenue? If you're not sure, if you don't remember, draw some graphs. Draw an inelastic, draw an elastic, figure it out. Okay, let's see. What happens? Revenue increases, right? If you have an inelastic demand curve and price goes up, revenue goes up as well.
Here's an application. Why is the war on drugs so hard to win? Well, drugs are typically going to have a fairly inelastic demand curve. What that means is that when enforcement actions raise the price of drugs, make it more costly to get drugs, raising the price, that means the total revenue for the drug dealers goes up. So check out this graph. Here is the price with no prohibition, here's our demand curve, our inelastic demand curve. What prohibition does, is it raises the cost of supplying the good. But that raises the price, which is what it's supposed to do, and that does reduce the quantity demanded of the drug. But it also has the effect of increasing seller revenues. And seller revenues may be where many of the problems of drug prohibition come from. It's the seller revenues which drive the violence, which drive the guns, which make it look good to be a drug dealer, which encourage people to become drug dealers, and so forth. So there's a real difficulty with prohibition, with prohibiting a good, especially when it has an inelastic demand.
Here's another application of elasticity of demand and how it can be used to understand our world. This is a quotation from 2012 from NPRs food blog "The Salt." "You've all heard a lot about this year's devastating drought in the Midwest, right? US Department of Agriculture announced last Friday that the average US cornfield this year will yield less per acre than it has since 1995. Soybean yields are down, too. So you think that farmers who grow these crops must be really hurting. And that's certainly the impression you get from media reports. But how's this, for a surprising fact? On average, corn growers actually will rake in a record amount of cash from their harvest this year." So can you explain this secret side of the drought? I'm not going to answer this question. This is exactly the type of question you might receive on an exam. But you should be able to answer it by now, with a few sketches on a piece of paper. And in particular, what I want you to answer is, what type of demand curve, for corn, would make exactly this type of outcome perfectly understandable? Not a secret or surprise, but perfectly understandable.
Okay, that's the elasticity of demand. Next time we'll be taking up the elasticity of supply, and we'll be able to move through that material much quicker because it covers many similar concepts. Thanks.
Subtitles
- English
- Spanish
- Chinese
- Hindi
- French
- Arabic
Thanks to our awesome community of subtitle contributors, individual videos in this course might have additional languages. More info below on how to see which languages are available (and how to contribute more!).
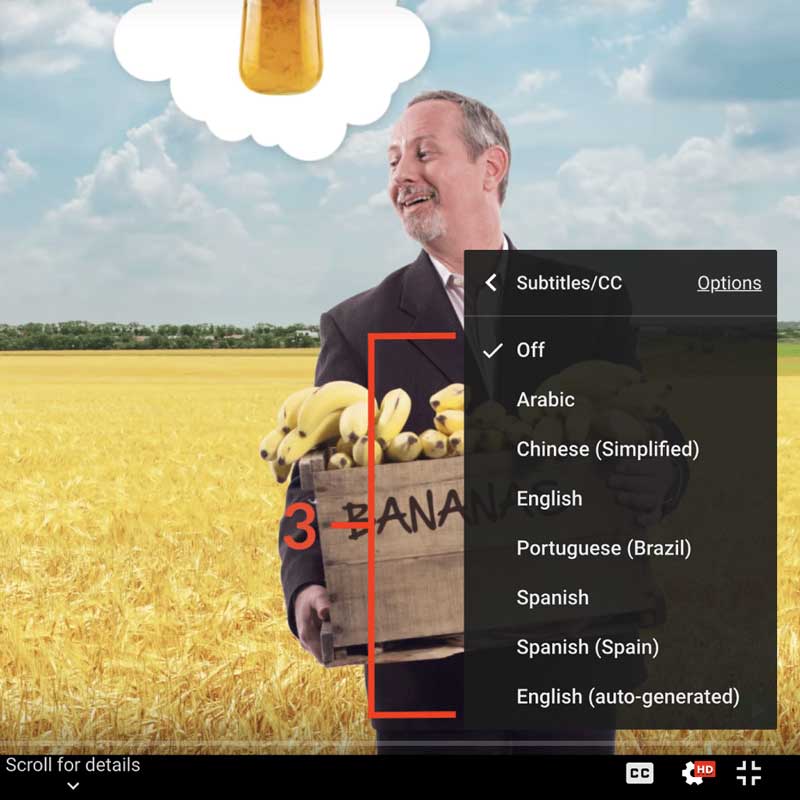
How to turn on captions and select a language:
- Click the settings icon (⚙) at the bottom of the video screen.
- Click Subtitles/CC.
- Select a language.

Contribute Translations!
Join the team and help us provide world-class economics education to everyone, everywhere for free! You can also reach out to us at [email protected] for more info.
Submit subtitles
Accessibility
We aim to make our content accessible to users around the world with varying needs and circumstances.
Currently we provide:
- A website built to the W3C Web Accessibility standards
- Subtitles and transcripts for our most popular content
- Video files for download
Are we missing something? Please let us know at [email protected]
Creative Commons

This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
The third party material as seen in this video is subject to third party copyright and is used here pursuant
to the fair use doctrine as stipulated in Section 107 of the Copyright Act. We grant no rights and make no
warranties with regard to the third party material depicted in the video and your use of this video may
require additional clearances and licenses. We advise consulting with clearance counsel before relying
on the fair use doctrine.

