Office Hours: Game Theory
Course Outline
Office Hours: Game Theory
In game theory, the Nash equilibrium is a concept that can help you analyze the behavior and outcomes of two or more people in a non-cooperative situation. The Nash equilibrium means that no person has an incentive to change their behavior or strategy, unless someone else changes their behavior or strategy.
For our Office Hours example, we’re going to look at a case involving two magicians, Bob and Al. If they both agree to only perform one show per week, they’ll rake in $10,000 each. But one or both could always cheat and perform more shows per week in an attempt to earn more money.
Now, to find the Nash equilibrium in this scenario, we’ll have to analyze Bob’s behavior based on Al’s behavior. And then we’ll have to analyze Al’s behavior based on Bob’s.
Check out this video and you’ll have the Nash equilibrium down in just a few minutes.
Teacher Resources
Related to this course
See all Teacher Resources related to this course
Transcript
Today, we're going to learn more about Game Theory by using it to solve a simple problem.
Bob and Al are two prestigious rival magicians who have developed a new trick that is quite popular. They've then agreed to limit performances so they can charge more. If both magicians perform only one show a week, each will earn $10,000. However, if one magician breaks the agreement and performs five times a week while the other continues to perform once a week -- that double-crosser will make $15,000 while the other magician will make only $1,000. And if both magicians break the agreement and perform five times a week, each will earn $6,000.
So, what is the Nash equilibrium of how many shows they will each perform?
The Nash equilibrium means that no person has an incentive to change their behavior or strategy unless someone else changes their behavior or strategy. In order to find the Nash equilibrium of Bob and Al's performances, we have to first analyze Bob's behavior based on Al's behavior and vice versa.
It will be easier to track everything if we fill out a 2-by-2 matrix. There are two individuals with two options. In each box of the matrix we'll list each person's path given the state of the world. So we'll list Bob's path first and Al's second. So let's first look at Bob's best strategy based on Al's behavior. Al will either keep her promise to perform once a week, or she'll break her promise and perform five shows. If she cooperates and performs one show, what is Bob's best strategy? Again, if we just look at what he stands to gain, then his best option would be to cheat and perform five times a week and make $15,000 versus performing once a week and making $10,000.
Now, what if Al backstabs Bob and performs five shows? Bob's best strategy here is also to perform five shows a week and make $6,000 versus performing once a week and making only $1,000. Given that Bob's best strategy is to cheat and perform five shows regardless of what Al does, cheating is his dominant strategy.
Now, let's look at it from Al's perspective. I bet you can see where this is going. If Bob keeps his promise and performs one show per week, then Al's best option is to perform five shows. She'll earn $15,000 instead of $10,000. And, if Bob decides to break his promise and perform five shows, Al's best option is also to cheat and perform five shows because she'll earn $6,000 instead of $1,000. Given that Al's best strategy is to perform five times per week -- again, regardless of what Bob does -- this is also considered her dominant strategy.
So if Bob's dominant strategy is to cheat as well, then the Nash equilibrium in this game is for both of them to break their promises. They'll each perform five shows and earn $6,000. Notice that this isn't an optimal outcome. It would be so much better for them to each perform only one show per week. They'd earn a lot more money, and they'd also have a lot more free time on their hands. But if we're just evaluating what to do from the payoffs listed in our matrix, it is in both Bob's best interest and Al's best interest to cheat. Thus, it's the Nash equilibrium.
Of course, there's a real world outside of the matrix. The world is much more complicated than this. People care about keeping promises, and they think about the long run, rather than just week to week. So think of this example as just a simple but powerful starting point to better understand human decision-making.
As always, let us know what you think. And, if you'd like more practice, check out our additional challenge questions at the end of this video.
Subtitles
- English
- Spanish
- Chinese
- Hindi
- French
- Arabic
Thanks to our awesome community of subtitle contributors, individual videos in this course might have additional languages. More info below on how to see which languages are available (and how to contribute more!).
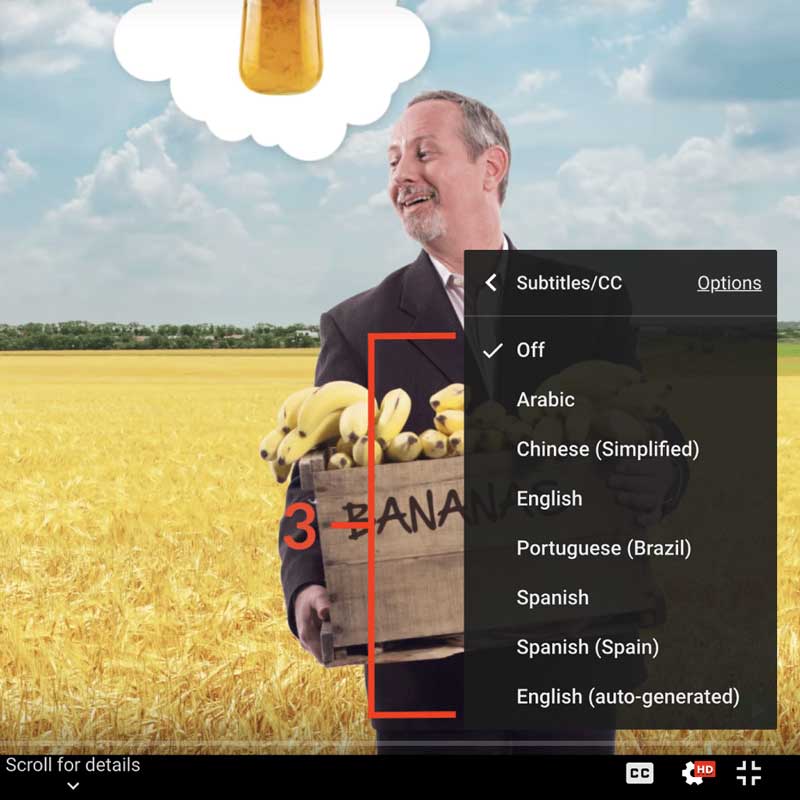
How to turn on captions and select a language:
- Click the settings icon (⚙) at the bottom of the video screen.
- Click Subtitles/CC.
- Select a language.

Contribute Translations!
Join the team and help us provide world-class economics education to everyone, everywhere for free! You can also reach out to us at [email protected] for more info.
Submit subtitles
Accessibility
We aim to make our content accessible to users around the world with varying needs and circumstances.
Currently we provide:
- A website built to the W3C Web Accessibility standards
- Subtitles and transcripts for our most popular content
- Video files for download
Are we missing something? Please let us know at [email protected]
Creative Commons

This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
The third party material as seen in this video is subject to third party copyright and is used here pursuant
to the fair use doctrine as stipulated in Section 107 of the Copyright Act. We grant no rights and make no
warranties with regard to the third party material depicted in the video and your use of this video may
require additional clearances and licenses. We advise consulting with clearance counsel before relying
on the fair use doctrine.

