Quantity Theory of Money
Course Outline
Quantity Theory of Money
This is "Quantity Theory of Money" from our Principles of Economics: Macroeconomics course.
The quantity theory of money is an important tool for thinking about issues in macroeconomics.
The equation for the quantity theory of money is: M x V = P x Y
What do the variables represent?
M is fairly straightforward – it’s the money supply in an economy.
A typical dollar bill can go on a long journey during the course of a single year. It can be spent in exchange for goods and services numerous times. In the quantity theory of money, how many times an average dollar is exchanged is its velocity, or V.
The price level of goods and services in an economy is represented by P.
Finally, Y is all of the finished goods and services sold in an economy – aka real GDP. (If you need a refresher on GDP, head back to the first section of the course). When you multiply P x Y, the result is nominal GDP.
Actually, when you multiply M x V (the money supply times the velocity of money), you also get nominal GDP. M x V is equal to P x Y by definition – it’s an identity equation.
You can think about the two sides of the equation like this: the left (M x V) covers the actions of consumers while the right (P x Y) covers the actions of producers. Since everything that is sold is bought by someone, these two sides will remain equal.
Teacher Resources
Transcript
Today we're going to introduce an important tool for thinking about issues in macroeconomics -- the quantity theory of money. Let's imagine the journey a dollar bill might take in a year. Imagine that the dollar bill starts with Tyler, who buys a pupusa from Don, the street vendor. Don gives it to his daughter, who spends it on a pony ride at the fair. It ends up in the hands of Alex, who, after losing it and then finding it in his couch cushions, buys a cup of coffee while on a road trip to see his favorite polka band. So, in a year, this dollar has been spent three times -- on the pupusa, the pony ride, and on a cup of coffee.
Okay, we've got the building blocks to understand the quantity theory of money already. Our dollar bill -- well, that's money, which we represent with the letter "M" -- how many times that dollar gets used in a year is called the “velocity of money,” which we'll label with a "V." In this case, V is 3, as our bill was spent three times in a year. The pupusa, pony ride, and coffee are real goods and services, which we'll call "Y." And the price of those goods and services, we'll call "P." These are the variables in the quantity theory of money.
Now, let's think about this for an economy as a whole. M would be the money supply -- all the money in the economy. V would be how many times a dollar is spent purchasing finished goods and services. Some people hoard cash under their mattress so their dollars have a low velocity, while others spend or invest their money quickly and their dollars have a high velocity. V is the number of times the average dollar is spent. P would the price level of all finished goods and services in an economy, and Y would be all the finished goods and services sold in an economy. So, Y is real GDP, and when you multiply it by a measure of the price level, you get nominal GDP.
Same thing over here. You take all our money, M, and multiply it by how many times the average dollar was spent, or V, and you get nominal GDP as well. Both sides represent nominal GDP in a different way. So, these are equal by definition, which is why we call this equation an identity. One way to think about it is that how much money we have in total times how many times the money is spent covers the actions of buyers. The stuff we sell times the prices we charge covers the actions of sellers. Given that everything that is sold is, by definition, bought by someone, this equation is true by definition. There are important questions about the variables and how they are measured. How do we measure M, for example? However, the core identity, that M times V must equal P times Y, gives us a lot of insight, and a way of organizing our thought about important macroeconomic issues.
So, we'll return to this tool often. For example, what can this identity equation tell us about the causes of inflation? That's the topic we'll turn to next.
Subtitles
Thanks to our awesome community of subtitle contributors, individual videos in this course might have additional languages. More info below on how to see which languages are available (and how to contribute more!).
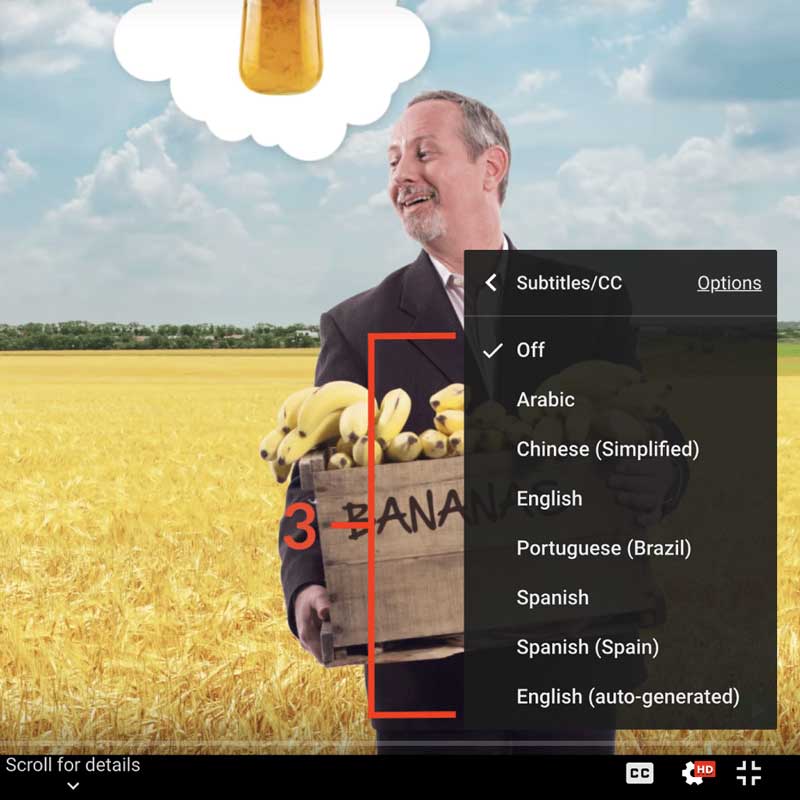
How to turn on captions and select a language:
- Click the settings icon (⚙) at the bottom of the video screen.
- Click Subtitles/CC.
- Select a language.

Contribute Translations!
Join the team and help us provide world-class economics education to everyone, everywhere for free! You can also reach out to us at [email protected] for more info.
Submit subtitles
Accessibility
We aim to make our content accessible to users around the world with varying needs and circumstances.
Currently we provide:
- A website built to the W3C Web Accessibility standards
- Subtitles and transcripts for our most popular content
- Video files for download
Are we missing something? Please let us know at [email protected]
Creative Commons

This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License.
The third party material as seen in this video is subject to third party copyright and is used here pursuant
to the fair use doctrine as stipulated in Section 107 of the Copyright Act. We grant no rights and make no
warranties with regard to the third party material depicted in the video and your use of this video may
require additional clearances and licenses. We advise consulting with clearance counsel before relying
on the fair use doctrine.

